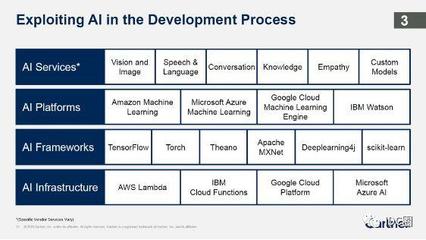
人工智能（AI）作為當今科技領域的前沿技術，正深刻改變著軟件開發的方式與效率。其中，線性回歸模型作為機器學習中最基礎且廣泛應用的算法之一，為AI軟件開發提供了堅實的理論基礎與實踐工具。

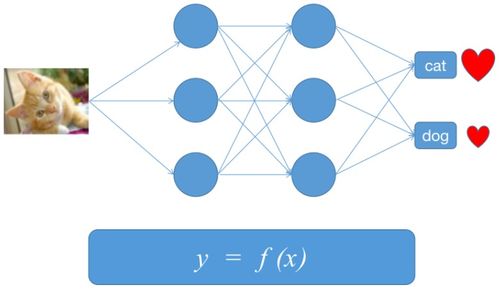
在人工智能基礎中，線性回歸模型通過建立自變量與因變量之間的線性關系，實現對數據的預測與分析。其數學表達式為 y = β? + β?x? + ... + β?x? + ε，其中y代表預測值，x為特征變量，β為模型參數，ε為誤差項。這一簡潔而強大的模型形式，使其成為眾多復雜AI系統的構建基石。

在軟件開發實踐中，線性回歸模型的應用主要體現在以下幾個方面：

在數據預處理階段，開發者可利用線性回歸進行特征重要性分析，識別對目標變量影響最大的因素，從而優化特征工程過程。例如在電商推薦系統開發中，通過分析用戶行為特征與購買意愿的線性關系，可有效提升推薦準確率。

在模型原型開發階段，線性回歸常作為基準模型，為后續更復雜的神經網絡或集成學習模型提供性能對比參考。其訓練效率高、解釋性強的特點，使其特別適合在項目初期進行快速驗證和迭代。

在工業級AI系統開發中，線性回歸模型因其穩定性和可解釋性，常被用于風險評估、銷量預測等關鍵業務場景。結合現代軟件開發框架如TensorFlow、PyTorch或Scikit-learn，開發者能夠快速實現模型的部署與集成。

值得注意的是，雖然線性回歸模型相對簡單，但在實際軟件開發中仍需考慮多重共線性、異方差性等問題。開發者需要通過正則化、特征標準化等技術手段優化模型性能，同時結合交叉驗證等方法確保模型的泛化能力。

隨著AI技術的不斷發展，線性回歸模型也在持續演進。多項式回歸、嶺回歸等變體形式的出現，進一步拓展了其應用范圍。在當今的AI基礎軟件開發中，理解并熟練運用線性回歸模型，已成為開發者必備的核心技能之一。

線性回歸模型作為人工智能領域的基礎算法，不僅為復雜AI系統開發提供了重要支撐，更通過其簡潔性和可解釋性，幫助開發者構建更加可靠、高效的軟件解決方案。在未來的AI軟件開發浪潮中，這一經典模型仍將發揮不可替代的作用。